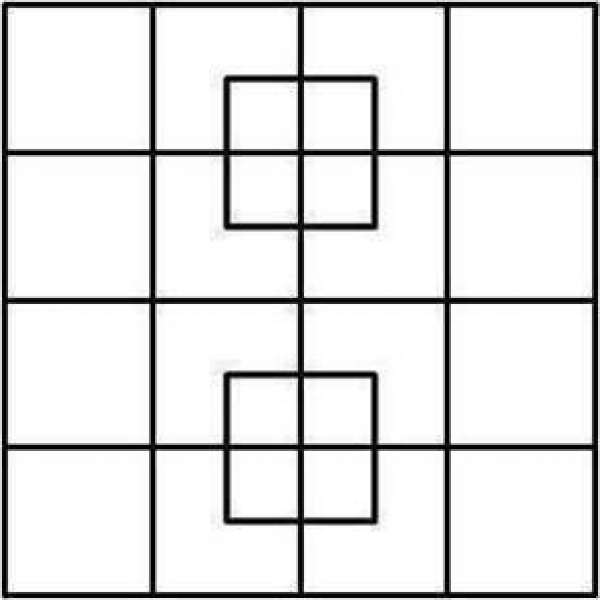
Açıklamalı bir cevap arıyorum.

gördüm ve arttiriyorum: 40
aciklama: teker teker sayiyorsun iste.


ben 40 saydım,ama cevap 40 da değil galiba.cevabı bilmiyorum.


40 tane


16 ya da 40.
eğer siyahlar çizgi (yani 1 boyutlu ise) ise 40.
eğer siyah çizgiler iki boyutlu ise (yani uzunluğuun dışında kalınlığı da varsa) sadece beyazlar kare oluşturur. o zaman 16.


38 tane var. dogruysa aciklayayim


40 tane.
Her birinde 16şar var 2 tane ayrı ayrı alırsak altı üstü. Bir de birleştirince ortada var bulduklarımız. 40 ediyor.


37 tane var.
sayarak bulunur.


saydım 40.


41.


a*a satır ve sütundan oluşmuş bir karedeki toplam kare sayısının kısaca formülü şudur. bu arada bu formülü üstün dehamla buldum :) benden önce muhakkak birileri keşfetmiştir.
1^2+2^2+3^2...a^2
örneğin bir satranç tahtasındaki kare sayısı
1^2+2^2+3^2...8^2 dir.
sorunun cevabına gelirsek; öncelikle şimdilik ortalardaki iki kareyi saymazsak 4*4 bir karede,
1^2+2^2+3^2+4^2=1+4+9+16=30 tane kare vardır. ortalardaki iki karede,
4+4+1+1=10 tane kare vardır.
30+10=40 tane kare vardır.


16+9+4+1+8+2=40
eger su ortadaki -duzeni bozan- kareler olmasa 30 olacakti. formulasyonu mmrsrkn'nin belirttigi gibi.


öss permütasyon yav. elin herifi de para istiyor anladığım kadarıyla :D


40