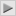soru bu arkadaslar. Şekildekiler her biri kare. paintte çizdiğim için böyle çakma görünüyo ama her biri kare. nasıl yapıyoruz bu tip soruları?
teşekkürler şimdiden.

mesela A'dan B'ye giden yatay yollara x diyeceksin, dikey yollara y.
(x+y)!/(kaç tane x varsa)!.(kaç tane y varsa)!
sonra B'den C'ye gidenlere de aynısını uygulayıp. ikisini çarpıcaksın.
bu kadar. anlamadıysan buradayım :)


@mor.inek
anladım. yapalım birlikte;
A'dan B'ye
x=3(yatay yollar)
y=4(dikey yollar)
(7!/3!x4!) = 35
B'den C'ye
x=3(yatay)
y=3(dikey)
(6!/3!x3!)=20
20*35=700yol mu?
şıklar : 50 - 60 - 75 - 80 - 90
ben anladım senin yöntemi, tekrarlı permutasyon gibi düşün diyosun da çarparsak olmuyo gibi, toplasak da şıklarda yok. gerçi çakma bi kitap bu çalıştığım, şıklar hatalı olabilir. cvp 60 diyo bu arada.


A ile B arası: 2 dikey 3 yatay 5!/(2!.3!)=10
B ile C arası: 2 dikey 2 yatay 4!/(2!.2!)=6
10.6=60
Yöntemin sağlamasını B C arasınıdaki yolları tek tek elle sayarak kontrol edebilirsin
edit: düzelttim :p


@Huan
A ile B arası: 2 dikey 3 yatay
B ile C arası: 2 dikey 2 yatay
nasıl? nasıl, 2 dikey yol var? nasıl sayıyoruz biz bu yolları


@Huan'ın söylediği cevap doğru ama işlemi yazarken heralde yanlışlık yapmış. :)
5!/(2!.3!) ve 4!/2!.2! işlemlerinde çarpım yerine toplam yazmış.Belirteyi dedim. :)