Merhaba. Endüstri mühendisliği/optimizasyon ile ilgili bir sorum var.
Normalde bir fonksiyonun türevini alıp 0'a eşitleyince max/min noktasını bulabiliyoruz. Bunu yapmak için fonksiyonun concave olması gerekiyor. Sorum şu ki elimdeki fonksiyon concave değil unimodal. Hala bir max/min noktası bulunuyor, yani fonksiyon optimize edilebiliyor. Hoca demiş ki bu fonksiyonun concave olması gerekmediğini gösterin. Ben bunu ders notlarından biliyorum, ama matematiksel olarak nasıl gösterebilirim?
Biraz karışık oldu ama sorunuz varsa açıklarım:)

sonuna kadar iyi gitmişsin ama hocanın ne sorduğu tam anlaşılmıyor.
concave olmayan bir fonksiyonun da optimize edilebildiğini ispatlayın mı diyor? anlamsız bir soru olur bu.
concave olmayan bir fonksiyonun da türev kullanılarak optimize edilebildiğini ispatlayın mı diyor?
yoksa bambaşka bir şey mi?


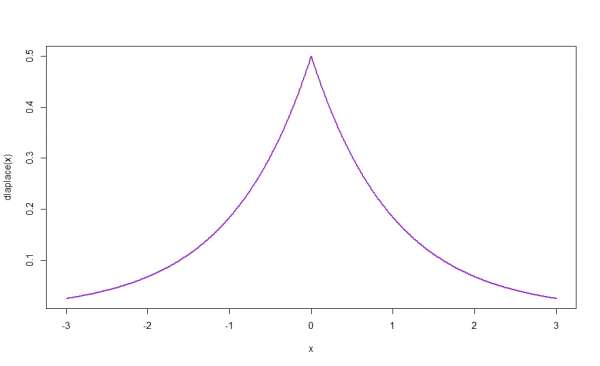
concave olmayan bir fonksiyonun da optimize edilebildiğini ispatlayın diyor. şimdi bir foto koydum. mesela bu fonksiyonun max noktasında türevi yok, ama gene de optimize edilebiliyor. bunu gösterin demiş.


konkav değilse türevini alıp x=0 dersen, /0 veya ∞ çıkar. onun için x=0 demek yerine x-->0 limit alarak max. min. noktasını bulabilirsin.


Max ve min 3 noktada aranır.
1. Türevin 0 olduğu noktalar.
2. Verilen aralığın uç noktaları
3. Türevin olmadığı noktalar (sağdan ve soldan türevin eşit olmadığı, eşit olsa bile o noktada tanımlanmayan fonksiyonlar)
Örneğin, ekte verdiğin fonksiyon x=0 noktasında türevlenemeyen bir fonksiyon. Bunun da kanıtı subgradient denilen kavramdan geçiyor. Şöyle bir teorem var: Eğer bir noktada türev tanımlı değilse ama subgradient aralığı 0 noktasını içeriyorsa, o nokta yerel veya global optimumdur. Fonksiyon unimodal olduğuna göre de bu nokta global optimumdur.
Subgradient şöyle bir şey, diyelim ki mutlak değer içinde x fonksiyonun var, bunun soldan gelen türevi -1, sağdan gelen türevi 1. Bu durumda subgradient aralığın [-1,1] ve 0'ı içeriyor ve fonksiyon da konveks; dolayısıyla bulunan nokta global min'dir. Aynı şey konkav fonksiyonda maksimizasyon için de geçerli.
Buradaki gibi konkavlık yoksa konik yaklaşım diye bir şey var. Fonksiyona aşağıdaki koni çizilir.
i.hizliresim.com 
Bu koninin de o noktada türevi yok, bu nedenle subgradient'e bakılır. Subgradient 0 noktasını içerdiği için de, o noktada bir optimum var denir.
Yalnız, bu lisans veya yüksek lisans konusundan çok öte. Bunun matematiksel ispatını Türkiye'de 10-15 kişiden fazlası yapamıyordur.
