[]
şekil sorusu
İlkokul 3 ten beri uğraşırım daha çizemedim şu şekli. eli kaldırmadan ve aynı çizgi üstünden tekrar geçmeden nasıl çizilir bu şekil ?
ya da esas soru çizilebilir mi ?
img174.imageshack.us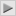
ya da esas soru çizilebilir mi ?
img174.imageshack.us
bi de bi gectigin yerden bi daha gecmıcen di mi
- bryan fury
(11.01.08 20:32:13)
evet tekrar geçmek yok
- kimlanbu (11.01.08 20:44:30)
cizilemez diye biliyorum.
- mandayuvasi (11.01.08 20:44:57)
imkansız
- ermanen (11.01.08 20:56:12)
Ortadaki çapraz çizgilerin biri eksik olmak üzere 1 yaklaşık sonuca puan veriliyor mu?
- inatci kahraman aga
(11.01.08 22:12:13)
evet evet, değişik kombinasyonlarla 1 yaklaşık oluyor, ya kenar çizgilerinde biri yada içerdeki çapraz çizgilerden biri kalıyor.
- crayze horse (11.01.08 22:35:22)
bende bu şeklin içinden çıkamadım daha
hatta bende ilkokul 3'ten beri.
x'ten y'ye gidicez ama bir karden sadece bir kere gecebilecegiz ve capraz gitmek yok!
x'ten başlayıp y'de bitirecegiz.
img527.imageshack.us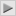
hatta bende ilkokul 3'ten beri.
x'ten y'ye gidicez ama bir karden sadece bir kere gecebilecegiz ve capraz gitmek yok!
x'ten başlayıp y'de bitirecegiz.
img527.imageshack.us
- etna (11.01.08 22:54:52)
1 yaklaşık sonuç oldukça farklı şekillerde elde edilebiliyor ne yazık ki puan verilmiyor :)
- kimlanbu (11.01.08 22:59:38)
etna'nın sorusunu tam anlayamadım, bütün karelerden geçmek zorunda mıyız? kareleri oluşturan çizgilerden mi gidicez? nasıl abi?
- crayze horse (11.01.08 23:14:35)
ekte gozuken resim için o dediginiz imkansız. daha 100 yıl ugrassanız bulamazsınız. ya o kulakcıklardan birini cıkaracaksınız ya da bakan biri icin ufak bi aldatmaca ile cizmiş taklidi yapma taktigini verebilirim:) dik dik bakan biriyse hooop elini kaldırdın diyo ama olsun:D
- rurouni (12.01.08 00:52:54)
Teorik olarak imkansız. Tek sayıda çizgi çıkan en fazla iki nokta olmalı, bunda dört nokta var. Kimse boşuna kasmasın.
- harzem (12.01.08 13:13:48)
- eldarduil (12.01.08 14:44:04)
@eldarduil verdiğin linkte gösterilen çözüm yanlış çünkü son hamlede ilk çizilen çaprazın üstünden geçiyor. (geçtiğiniz yerden tekrar geçmeyiniz'e istinaden)
- lepidodendron (14.01.08 14:40:45)
geçilmiş yer demek. çizilen doğru parçasının tamamının üzerinden geçmek demektir. Benim verdiğim çözümde çizilen her doğru parçası diğer bir doğru parçasının noktalarını kullanmıyor. Doğru parçası iki nokta arasındaki en kısa yol olduğuna göre. Eğerki çizilmiş bir doğru parçasının belirtilmiş noktalarının her ikisinden de geçseydim üzerinden geçmek olurdu ki bu yapacağım hamle zaten gene aynı doğru parçasını verecektir bana.
kısaca ikinci çizilen çapraz çizgi ilk çizilen çapraz çizginin oluşturulduğu noktalardan hiçbirini kullanmamakta dolayısıyla aynı çizgi(doğru parçası) üstünden geçilmemiştir.
Çizgilerin kesişmeleri sayılmıyorsa ise (doğru parçalarının kesiştikleri yer bir nokta belirtir) çizgileri çizerken bir doğru parçasını oluşturmak için kullandığımız iki noktadan birini çizeceğimiz bir diğer doğru parçasının noktalarından biri olarak kullanıyoruz. o halde bununda üzerinden geçmek demek olması gerekir. Dolayısıyla soru çözümsüz kalır.
Benim çizdiğim şekilde doğru parçalarını çizmek için toplam 5 nokta kullanılıyor.
Ortadaki çapraz iki doğru parçasını birbirlerini kesmeyecek şekilde çizebilen varsa tadelle alıcam.
kısaca ikinci çizilen çapraz çizgi ilk çizilen çapraz çizginin oluşturulduğu noktalardan hiçbirini kullanmamakta dolayısıyla aynı çizgi(doğru parçası) üstünden geçilmemiştir.
Çizgilerin kesişmeleri sayılmıyorsa ise (doğru parçalarının kesiştikleri yer bir nokta belirtir) çizgileri çizerken bir doğru parçasını oluşturmak için kullandığımız iki noktadan birini çizeceğimiz bir diğer doğru parçasının noktalarından biri olarak kullanıyoruz. o halde bununda üzerinden geçmek demek olması gerekir. Dolayısıyla soru çözümsüz kalır.
Benim çizdiğim şekilde doğru parçalarını çizmek için toplam 5 nokta kullanılıyor.
Ortadaki çapraz iki doğru parçasını birbirlerini kesmeyecek şekilde çizebilen varsa tadelle alıcam.
- eldarduil (16.01.08 16:19:16)
1
